Interactions between Discrete and Continuous Optimization

Modern complex systems induce many optimization problems involving both discrete and continuous variables and constraints. Circuit layout in chip design demands place-and-route of hypergraphs (with discrete locations) that satisfies various integer or real constraints; optimizations in robotics must consider the interaction between discrete skill planning and piecewise-continuous optimal control. How can we inject learning to tackle mixed discrete and continuous optimization? Can methods from discrete and continuous optimization bootstrap each other? And, how do we translate these to practice?

Optimization: Distributed and Parallel

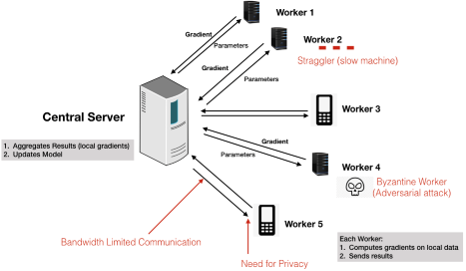In modern data-intensive applications, the size of training datasets has grown such that memory and processing power of a single server is not enough to unravel the underlying models or functional relationships in data. Thus, efficient algorithms are not enough for such optimization tasks: we need parallelizable algorithms. Can we make every optimization method distributedly implementable? How do the constraints of communication, privacy, fairness, and security affect the convergence rate of distributed optimization methods?

Optimization and Sampling on Geometric Spaces

Geometry is implicit in much of optimization, where it influences numerous models, algorithms, and applications. For example, numerous problems in robotics and vision applications, e.g., planning and SLAM, evolve on (nonlinear) manifolds. Examples of such spaces include Lie groups, homogeneous spaces, Grassmannians and Riemannian manifolds. While quite general, these manifolds often have rich structure and symmetries. Can we make explicit use of such manifolds to model real-world optimization problems? Can we design efficient algorithms for optimization and sampling on manifolds that leverage their geometric structure?

Sequential Learning and Decision Making

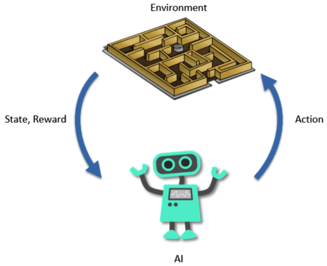In sequential decision making (e.g., robotics and automated network tuning), it is often crucial to balance exploration versus exploitation. Unlike offline or static problems, exploring the space and quantifying uncertainty are indispensable for informed decisions to be made. A major challenge in the exploration problem is the tradeoff between accuracy and computational budget. In particular, we need algorithms that scale well with the model complexity and can deal with an explosion in data as we make decisions. Can we advance sampling methods to facilitate the exploration problems in sequential decision making? Can we leverage special structures in sequential decision making problems to facilitate faster exploration?

Nonconvex Optimization (and Beyond) in Deep Learning

In recent years, deep learning (DL) models and methods have become key tools for a myriad of applications. The recent successes of DL hinge on efficient optimization of large, highly parameterized neural networks in practice. These problems are often nonconvex and pose a significant challenge as nonconvex optimization problems are in general computationally intractable. Can we understand and explain the efficiency of gradient-based nonconvex optimization methods for DL? How can the theoretical understanding be translated to better practical algorithms? One of the foremost challenges in advancement of AI is to be able to learn in the presence of stochastic or adversarial agents. This requires nonconvex optimization in a min-max setting. Can we build upon the successes of DL and extend the optimization framework to be able to perform nonconvex optimization in such settings?